​蝴蝶定理五大结论

蝴蝶定理五大结论

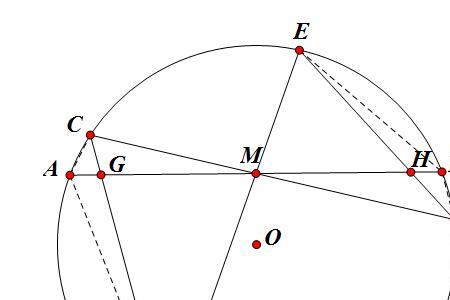
蝴蝶定理一共有四大结论！他们分别是：

一、蝴蝶模型中左右部分（翅膀）面积相等。

二、蝴蝶模型中对角线分开的相邻两个三角形的面积比相等

三、相对的两个三角形的面积的乘积相等

四、上下相对的两个三角形的面积比等于上下底 的平方比。

蝴蝶模型的四大结论如下:1、相似图形，面积比等于对边比的平方也就是:S1:S2=a^2/b^2。2、

S1:S2:S3: S4=a2: b2: ab: ab。 3、

S1xS2=S3xS4(由S1/S3=S4/S2推导出)。4、 A0:BO=(S1+S3):(S2+S4)。

蝴蝶定理(Butterfly Theorem)，是古代欧氏平面几何中最精彩的结果之一。

这个命题最早出现在1815年，由W.G.霍纳提出证明。而“蝴蝶定理”这个名称最早出现在《美国数学月刊》1944年2月号，题目的图形像一只蝴蝶。这个定理的证法不胜枚举，仍然被数学爱好者研究，在考试中时有各种变形。

霍纳证法:

过O作OLLED，OT丄CF，垂足为L、T

连接ON，OM，OS，SL，ST

可知/F=/D&ltC=ZE(同弧所对的圆周角相等)

ESD△CSF(AAA)

.DS/FS=DE/FC

根据垂径定理得:DL=DE/2，FT=FC/2

∴DS/FS=DL/FT

又·/D=/F

·∧DSLSAFST

./SLD=/STF

即/SLN=/STM

S是AB的中点所以OSLAB(垂径定理逆定理)

./OSN=/OLN=90°

N，!四点共圆(对角互补的四边形共

同理，0，T，M，S四点共圆

./STM=/SOM，/SLN=/SON(同弧所对的圆周角相等)

./SON=/SOM

∴&ltOTS=/OMS，&ltOLS=&ltONS(同弧所对的圆周角相等)

∴/OMS=/ONS

OSLAB

.在△OSM和△OSN

/MSO=/NSO

/OMS=/ONS

OS=0S

∴△SOM≌△SON (AAS)

∴MS=NS

作图法

从X向AM和DM作垂线，设垂足分别为X&#39和X&#34。类似地，从Y向BM和CM作垂线，设垂足分别为Y&#39和 Y&#34。

蝴蝶定理五大结论

蝴蝶定理（Butterfly Theorem）：设M为圆内弦PQ的中点，过M作弦AB和CD。设AD和BC各相交PQ于点X和Y，则M是XY的中点。

去掉中点的条件，结论变为一个一般关于有向线段的比例式，称为“坎迪定理”，不为中点时满足：1/MY-1/MX=1/MQ-1/MP ，这对2，3均成立。

蝴蝶定理是古典欧式平面几何的最精彩的结果之一。这个定理的证法不胜枚举，至今仍然被数学热爱者研究，在考试中时有出现各种变形。

蝴蝶定理最先是作为一个征求证明的问题，刊载于1815年的一份通俗杂志《男士日记》上。由于其几何图形形象奇特、貌似蝴蝶，便以此命名，定理内容：圆O中的弦PQ的中点M，过点M任作两弦AB，CD，弦AD与BC分别交PQ于X，Y，则M为XY之中点。